基尔霍夫定律

2015-01-25 11:28
19356
资讯文章
admin
来源：本站

一．名词介绍
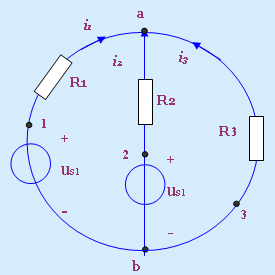
我们以图1-4-1所示的电路来介绍有关的名词。
1.支路：按狭义定义，把通过同一电流的电流路径成为
支路。如图1-4-1，该电路共有三条支路，其中支路

b1a和b2a中既有电阻又有电源，称为有源支路；
支路a3b只有电阻而无电源，称为无源支路。
   2.节点：按狭义定义，三条和三条以上支路的联接点
称为节点，如图1-4-1所始电路有两个节点a和b。
   3.回路：由支路构成的闭合路径称为回路，如图1-4-1，
共有三个回路，即a2b1a回路，a3b2a回路，a3b1a
回路。
    二．基尔霍夫电流定律（KCL）　　　　　　　　　
    基尔霍夫电流定律是描述电路中各支路电流之间相互关系的
的定律。在任意时刻t，流入某个节点的电流的总和等于流出该
节点的电流的总和。此结论称为基尔霍夫电流定律（KCL）。
例如对于图1-4-1所示电路，我们设定各支路电流的大小和参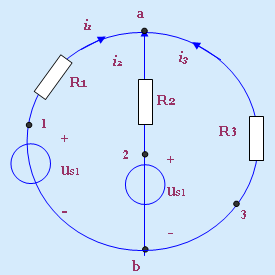             　　　　　　　　　　　
考方向如图中所示，则对该点有

　　　　　　 i1(t)+i2(t)=i3(t)
将上式改写为　-i1(t)-i2(t)+i3(t)=0
上式的物理意义是，流出节点a的电流的代数和等于零。这里流出的电流规定取正号，则流入的电流即取负号。

若将上式再改写为 i1(t)+i2(t)-i3(t)=0 图1-4-1 电路举例

此式的的物理意义是，流入节点a的电流的代数和等于零。这里流入的电流规定取正号，则流出的电流即取负号。
    上两式是KCL的另一中叙述法。它们本质上是一样的，只是在列写方程时把流出节点的电流规定为正，还是把流入节点的电流规定为正而已。
    上两式写成一般形式为：∑i1(t)=0 即集中在任一节点上的各支路电流的代数和恒为零。
    需要注意的是：在写方程时，如把流出节点的电流视为正，则流入节点的电流即需取为负；反之则反之。
    推广：KCL原是运用于节点的，但把它加以推广，也可使用于包围几个节点的闭合面。如图1-4-2所示电路中，闭合面S内有三个节点1，2，3。

图1-4-2 KCL推广于闭合面

当设定各支路电流的大小和参考方向如图中所示时，则对此三个节点即可列出KCL方程　　　　　

　　　　　　　　　　i1 = i12 - i31
　　　　　　　　　 i2= i23 - i12

　　　　　　　　　i3 = i31 - i23
把以上三式相加得： i1 + i2 + i3=0 或 ∑i1(t)=0
即流入（或流出）一个闭合面的支路电流的代数和恒等于零。此即广义的KCL。需要注意的是：在写方程时，如把流出闭合面的电流视为正，则流入闭合面的电流即需取为负；反之则反之。

[page]

三．基尔霍夫电压定律（KVL）
基尔霍夫电压定律是描述回路中各支路电压之间相互关系的定律。在任意时刻t，沿任一回路所有支路或元件上电压的代数和恒等于零，即　　 ∑u(t)=0 （1-4-2）
此结论称为基尔霍夫电压定律（KVL）。在写此方程时，应首先为回路设定一个饶行方向，凡电压的参考极性从"+"到"-"与回路绕行方向一致者，则该电压前取"+"号，否则取"-"号。
例如对于1-4-3所示电路，我们设定各元件电压的参考极性和回路的绕行方向如图中所示，则有
　　　　　　　 u1+u2+u3+us3-us4-u4=0
将此式改写为 -u1-u2-u3-us3+us4+u4=0
方程意味着把回路的绕行方向设定为与前者相反。由此可见，回路绕行方向的设定直接影响着方程中各项正负号的确定，但不影响方程的本质，故可以任意设定。

　
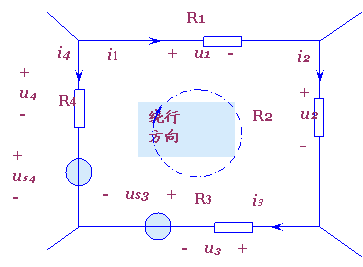
图1-4-3 电路中的一个回路

     若电路中的电阻均为线性电阻元件，则上述的KVL方程还可改写为另一种叙述方法，即
　　　　　　R1i1+R2i2+R3i3+ us3-us4-R4i4=0
即　　　　 R1i1+R2i2+R3i3-R4i4= -us3+us4
即　　　　∑Rkik=∑usk (1-4-3)
上式指出，任一回路中电阻上电压降的代数和恒等于电压源电压升的代数和。凡电流参考方向与回路绕行方向一致者，上式等号左端Rkik前取"+"号，不一致者，Rkik前取"-"号；凡电压源电压的极性从"-"到"+"与绕行方向一致者，上式等号右端usk前取"+"号，不一致者，usk前取"-"号。
    四．拓扑约束的概念
   基尔霍夫电流定律（KCL）描述了电路中各支路的电流之间的关系，基尔霍夫电压定律（KVL）描述了电路中各支路电压之间的关系，它们都与电路元件的性质无关，而只取决于电路的连接方式。所以我们把这种约束关系称为连接方式约束或拓扑约束，而把根据它们写出来的方程分别称为KCL约束方程和KVL约束方程。
至此，我们已经引入了两种约束的概念：元件约束与拓扑约束。它们贯穿着电路课程的始终。